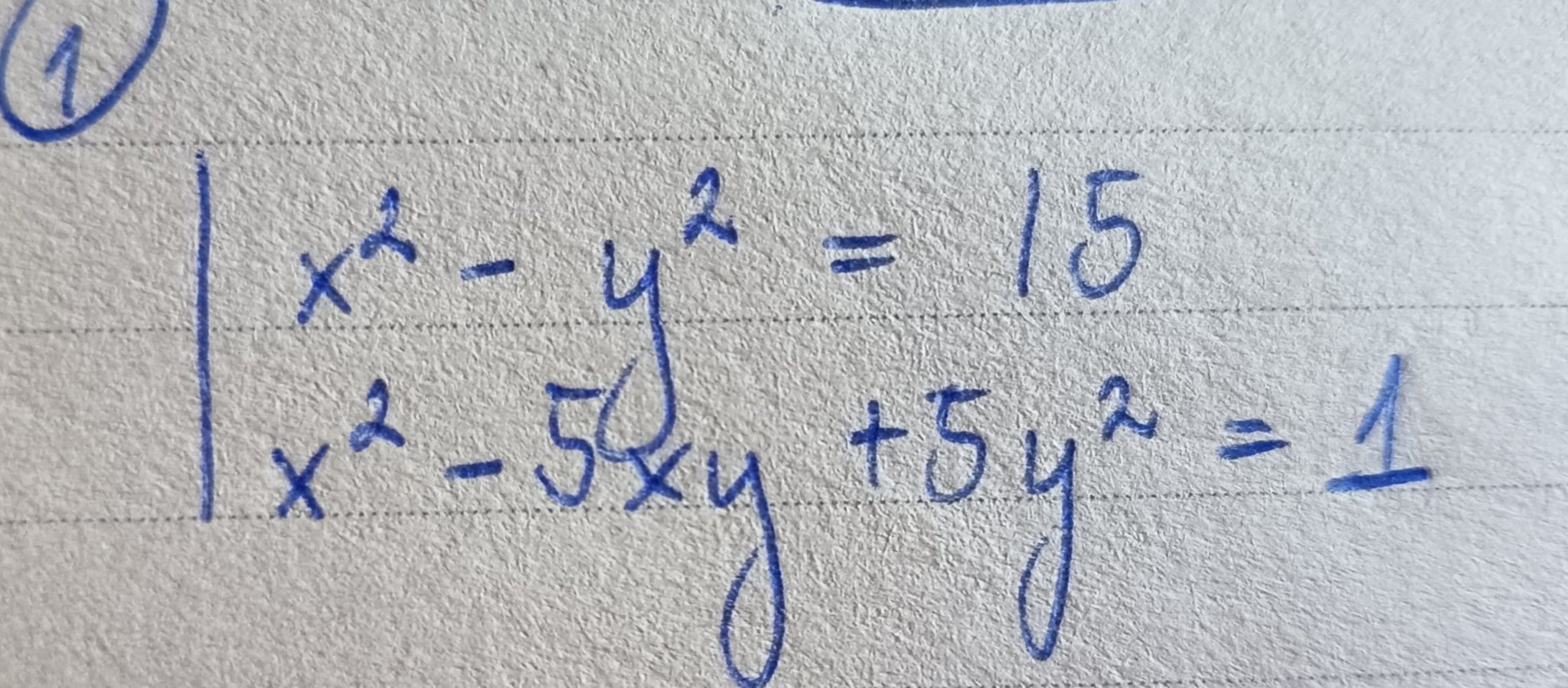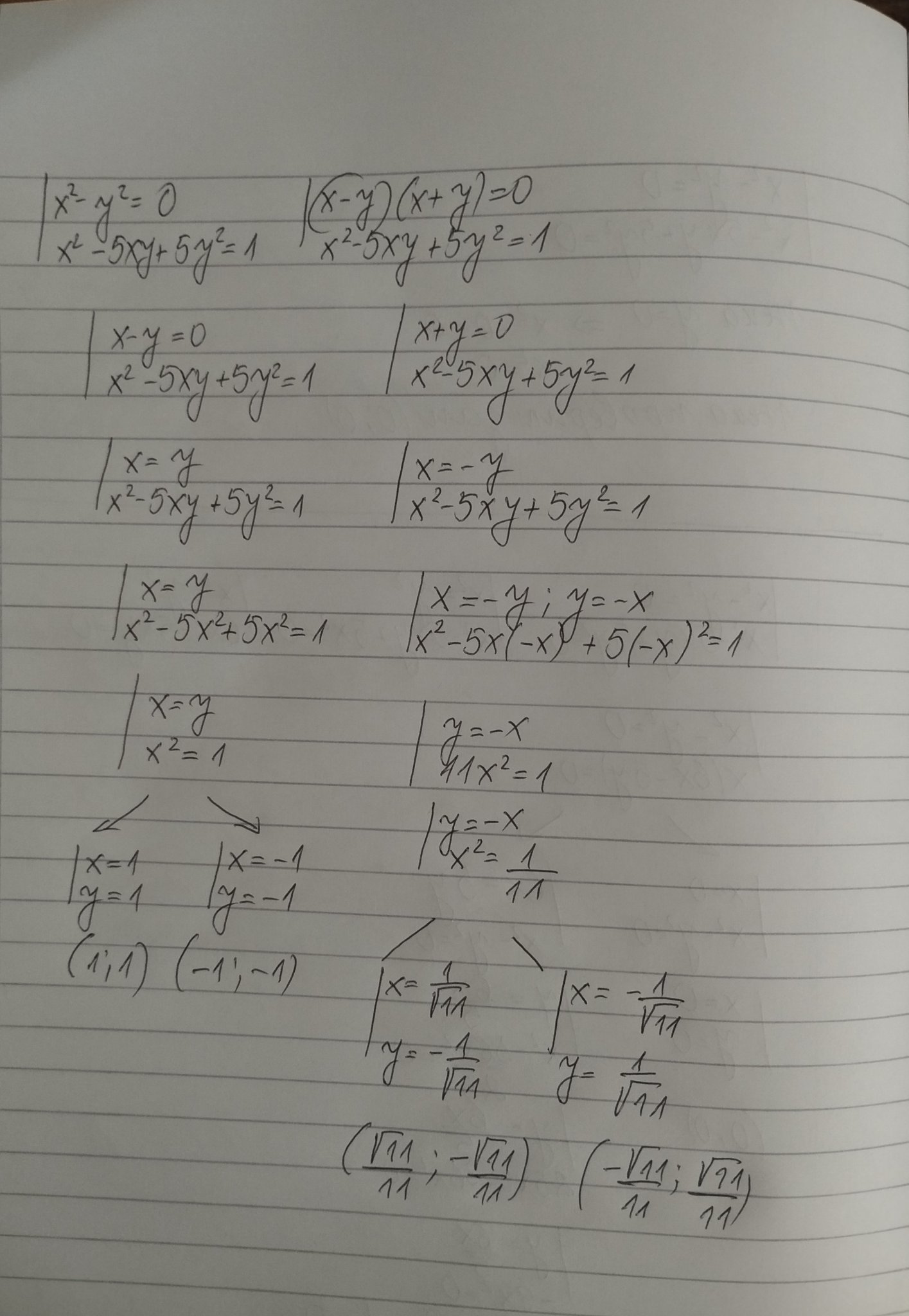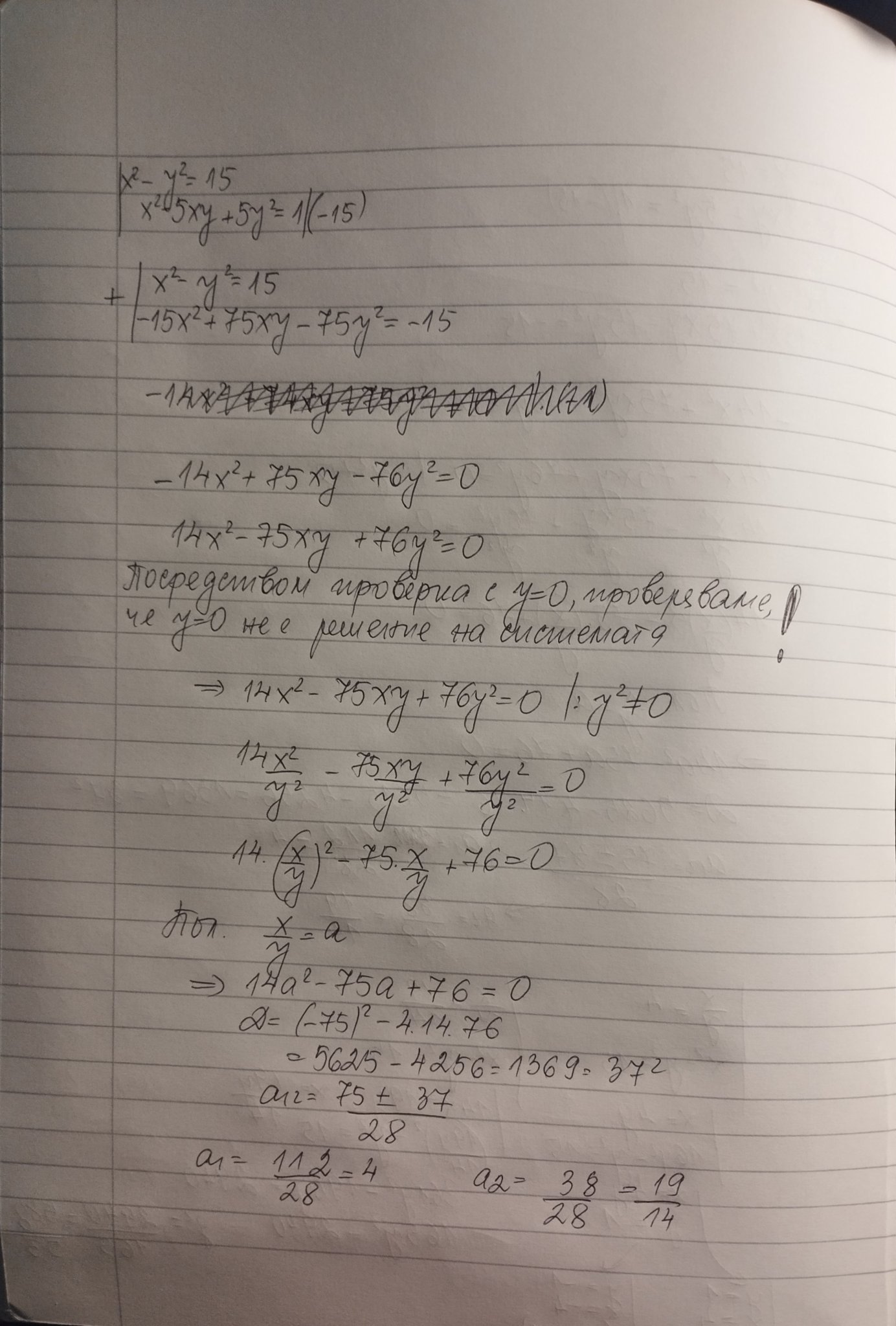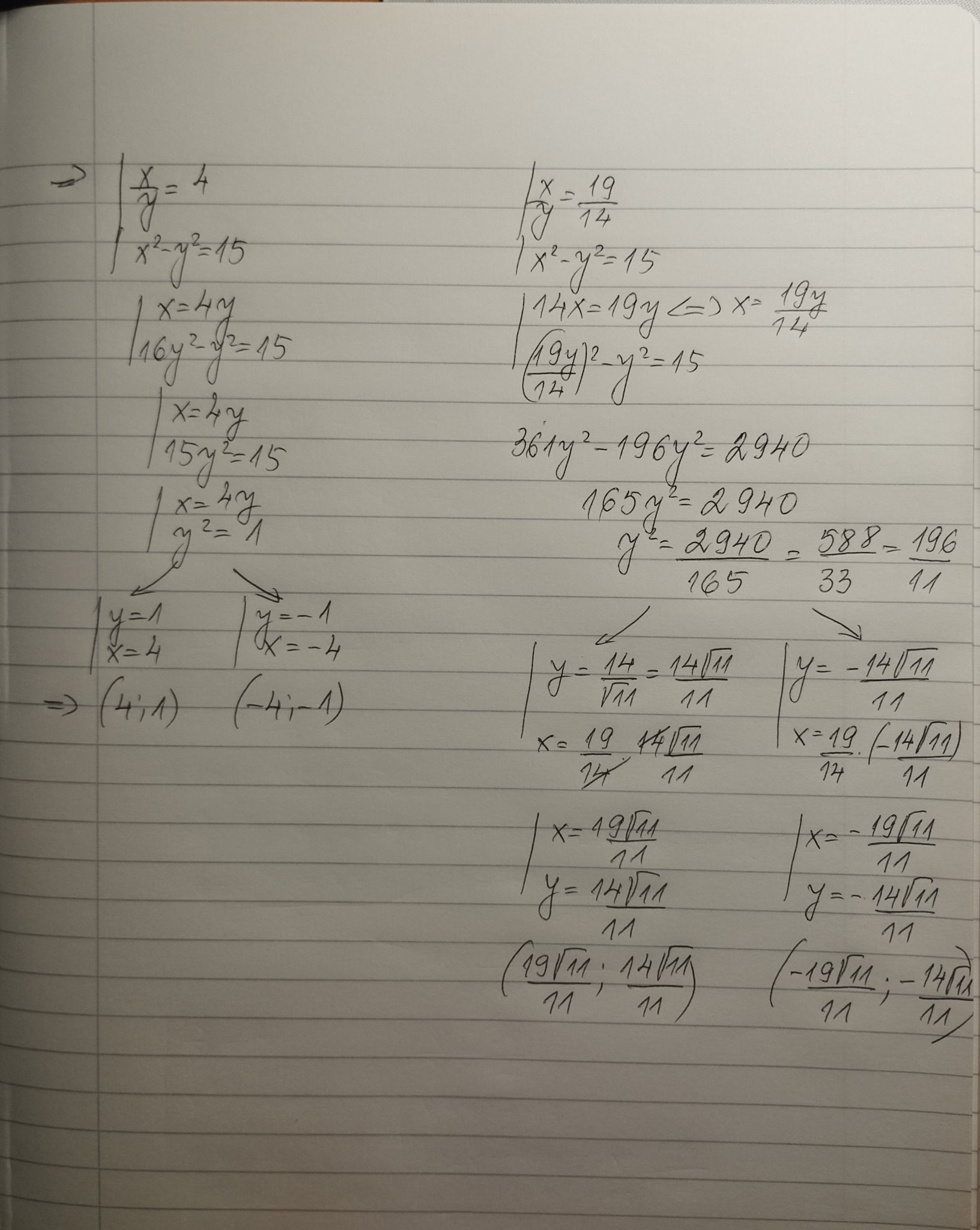Много ви благодаря! Хубава вечер!
- Публикувана: 4 дек. 2025, 18:45 ч.
- Последно мнение: 22 ян. 2026, 08:08 ч.
Задача някого препъва, в кофти сметки той затъва, тук има много помагачи за спъващите го задачи
Русалке, благодаря ти.
Исках да попитам само, защо х2-у2=0, а не на 15, както е в условието или това е пример?
Исках да попитам само, защо х2-у2=0, а не на 15, както е в условието или това е пример?
С уговорката,че ме мързи да я пререшавам,а нещо не ми харесват отговорите и може да съм омотала някоя сметка...
Идеята е,когато има произведение х.у,което не може да се премахне чрез събиране да се направят десните стр противоположни числа,та при събирането да се получи хомогенно уравнение от което да се изведе връзка между х и у-в учебника на Просвета за 9 кл има такива.
За 11. С тези лица имаш отношението АО:ОС=9:4. ВО:OD също е 9:4. S COD=16/9.
На 12. продължаваме бедрата. Нека се пресичат в т. Р. S PDC ako e a, a равните лица на МNDC и АBMN са b. Изразяваме отношенията на подобните триъгълници. а/(а+2b)=5^2/12^2. Намираме отношението а/b. Корен от a/(a+b) се явява CD/MN. MN получих, че е 13.корен от 2/2.
На 12. продължаваме бедрата. Нека се пресичат в т. Р. S PDC ako e a, a равните лица на МNDC и АBMN са b. Изразяваме отношенията на подобните триъгълници. а/(а+2b)=5^2/12^2. Намираме отношението а/b. Корен от a/(a+b) се явява CD/MN. MN получих, че е 13.корен от 2/2.
