Q&A
Обобщени въпроси и отговори от темата *
Как се решават задачи за движение, работа и други подобни за седмокласници?
Как се решават задачи с отрицателни числа за ученици от 5-ти клас?
Как се решават задачи с умножение на степени с една и съща основа?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Как се решават задачи за движение, работа и други подобни за седмокласници?
Задачите за движение и работа изискват внимателно разбиране на условието и използване на подходящи формули. Например, при задачи за движение използвайте формулата за изминат път: изминато разстояние = скорост * време. За работата е важно да разберете какво представлява работата и как се изчислява. Моля, предоставете задачите, за да ви помогнем с конкретни решения.
-
Как се решават задачи с отрицателни числа за ученици от 5-ти клас?
За учениците от 5-ти клас работата с отрицателни числа може да бъде представена чрез конкретни ситуации, като например температурни разлики или движение в различни посоки. Важно е да се подчертае, че отрицателните числа се използват за представяне на отрицателни стойности или посоки. Покажете ни конкретна задача, за да ви помогнем с подходящo обяснение и решение.
-
Как се решават задачи с умножение на степени с една и съща основа?
При умножение на степени с една и съща основа, използвайте свойствата на степента, които включват събиране на степени с еднаква основа и умножение на степени. Например, при умножение на x^2 * x^3, използвайте свойството x^m * x^n = x^(m+n). Покажете ни конкретна задача, за да ви помогнем с подходящo обяснение и решение.
-
Как се решават задачи за разлика и събиране на числа за трети клас ученици?
-
Как решават задачи за обем и вместимост за осми клас?


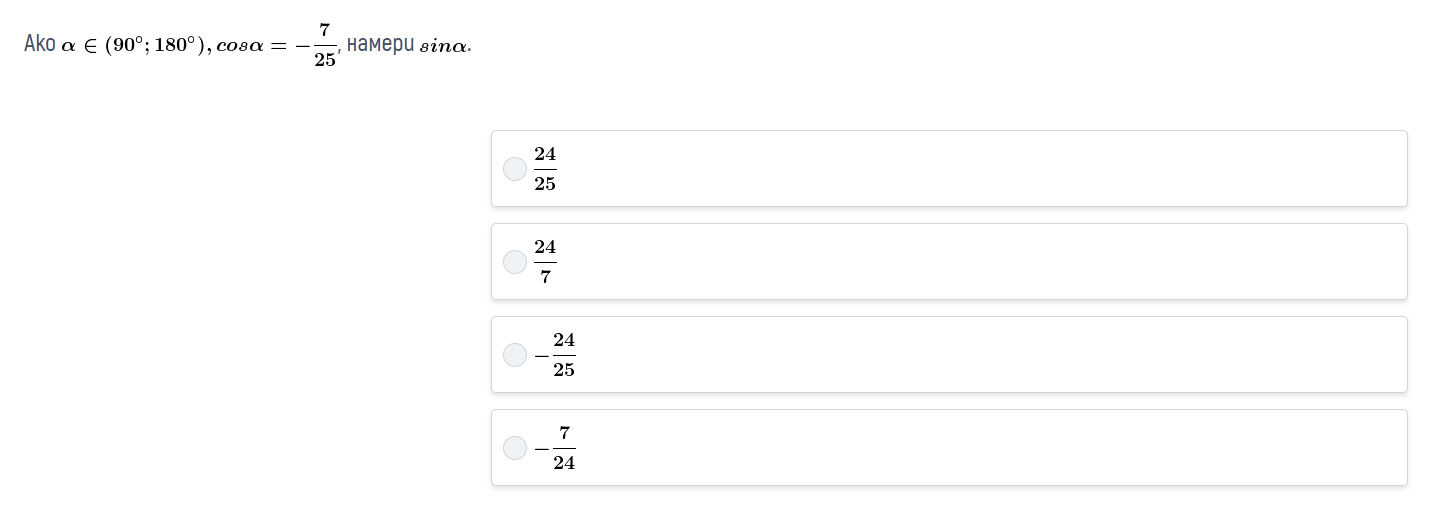


 Помощ за тези задачи🙏
Помощ за тези задачи🙏