Приемайки общите условия за ползване на сайта, потребителят се съгласява да се запознае с правилата и политиката за ползване на форума и да ги спазва, както и при ползването на сайта да съблюдава българското законодателство, интернет етиката, правилата на морала и добрите нрави.
НЕГ.БГ АД не гарантира за достоверността и пълнотата на съдържанието и не гарантира, че предоставените услуги ще удовлетворят изискванията на потребителя, нито че ще бъдат непрекъснати, навременни и сигурни. С приемането на общите условия потребителят се съгласява, че използването на предоставените услуги и информация е изцяло на негов риск и отговорност.
НЕГ.БГ АД няма задължение да извършва наблюдение на информация, публикувана от потребителите, както и на информацията, съхранявана, пренасяна или направена достъпна чрез сайта, нито да търси факти и обстоятелства, указващи извършването на неправомерна дейност от страна на потребител.
НЕГ.БГ декларира, че потребителските данни няма да бъдат предоставяни на трети лица, освен при поискване от съответните компетентни държавни органи или длъжностни лица, които са оправомощени да изискват такава информация съгласно действащото законодателство.
НЕГ.БГ АД си запазва правото да изпраща анкети за проучване и подобряване на удовлетвореността от предлаганите стоки и услуги, маркетингови проучвания с цел разработка и предлагане на нови стоки и услуги в сайта, както и непоискани търговски съобщения до регистрираните потребители с цел информиране за нови услуги и стоки, предлагани от дружеството.
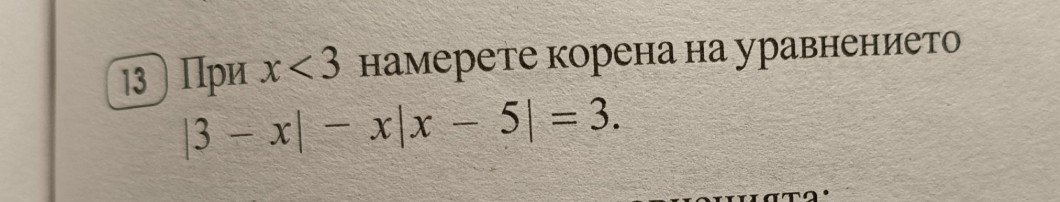
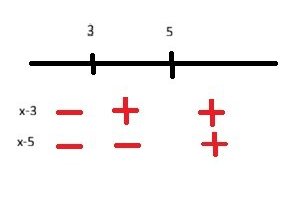
 , че ако има два модула в уравнение, се разкриват с противоположни знаци.
, че ако има два модула в уравнение, се разкриват с противоположни знаци.