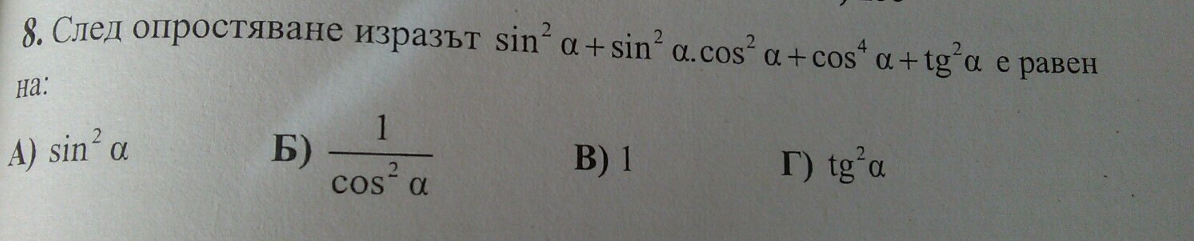Q&A
Обобщени въпроси и отговори от темата *
Каква е задачата с конус и вписана в него сфера, обсъждана във форума?
Каква е задачата с равнобедрен триъгълник и височини, равни на основата?
Как се решава задачата с триъгълник ABC, където ъгъл B е 45 градуса, върху BC е взета точка D, такава че CD = 2BD и ъгъл ADC = 60 градуса?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Каква е задачата с конус и вписана в него сфера, обсъждана във форума?
Задачата с конус и вписана в него сфера изисква намиране на ъгъла между образуващата и равнината на основата на конуса. При условие, че обемът на конуса е 4/9 от обема на сферата, се извеждат три възможни стойности за косинуса на въпросния ъгъл. Един отговор (180 градуса) се елиминира, тъй като не е остър ъгъл, а другите два (1/2 за 60 градуса и 1/5) остават валидни решения. Въпросът защо корекцията от 1/5 не се използва остава отворен, като се предполага, че учителят може да предпочете табличен ъгъл.
-
Каква е задачата с равнобедрен триъгълник и височини, равни на основата?
В задачата с равнобедрен триъгълник и височини, равни на основата, се изследва възможността, че ако двете височини в един триъгълник са равни на основата му, то той е равнобедрен. Това вярността на твърдението се доказва чрез изразяване на лицата по три начина и установяване на равенство между тях. По този начин се доказва, че триъгълникът е равнобедрен и оттам се извежда отговорът на въпроса.
-
Как се решава задачата с триъгълник ABC, където ъгъл B е 45 градуса, върху BC е взета точка D, такава че CD = 2BD и ъгъл ADC = 60 градуса?
За да разрешите задачата с триъгълник ABC, където ъгъл B е 45 градуса, върху BC е взета точка D, такава че CD = 2BD и ъгъл ADC = 60 градуса, се използват различни изрази на отношения между страните и ъглите в триъгълника. Чрез използване на свойствата на медианите се установява равенство между страните и се извежда отговорът на задачата.
-
Как се решава задача с два трактора, работещи заедно?
-
Каква е формулата за площта на триъгълник и кога се използва?