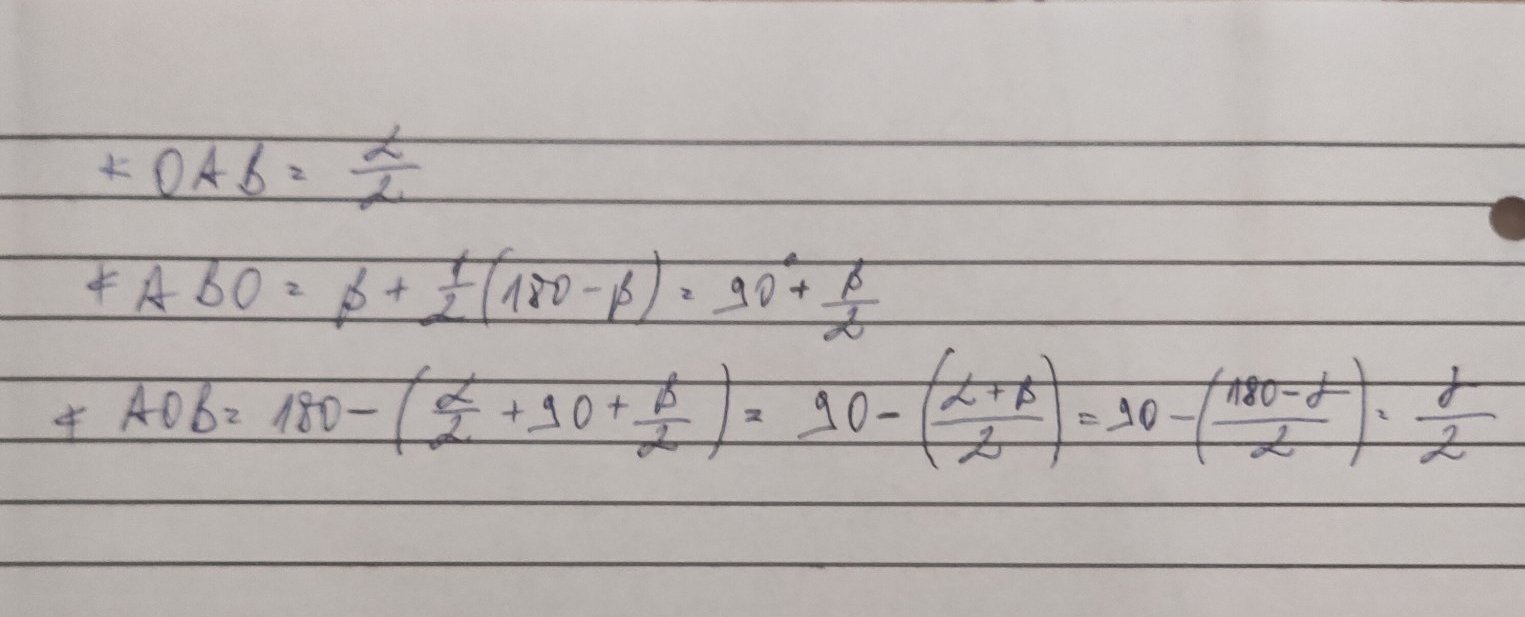Q&A
Обобщени въпроси и отговори от темата *
Каква е задачата, в която се използва формулата за съкратено умножение?
Как се решава задачата, в която трябва да се намерят ъгли в триъгълници?
Как се решава задачата за намиране на дължината на диагонала в трапец?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Каква е задачата, в която се използва формулата за съкратено умножение?
-
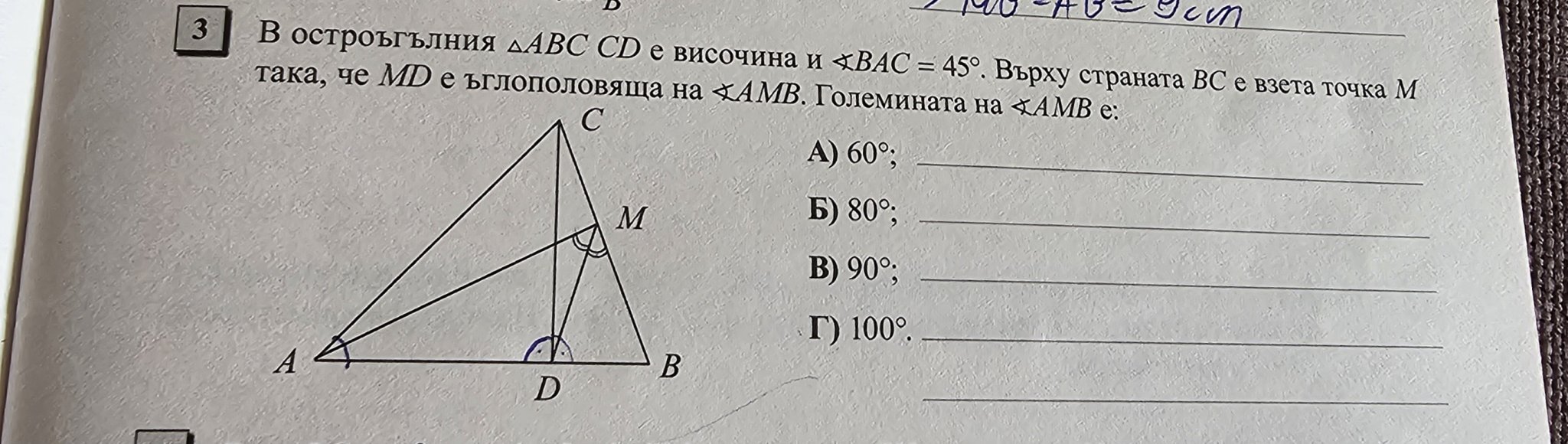
Как се решава задачата, в която трябва да се намерят ъгли в триъгълници?
За намиране на ъгли в триъгълници могат да се използват различни геометрични принципи. Например, при задачата за намиране на ъгли в триъгълници може да се използва принципът, че в тъпоъгълен триъгълник страната срещу тъпия ъгъл е по-дълга от другите страни. Освен това, за намиране на ъгли в триъгълници може да се използва и принципът за сравняване на дължини на страните в триъгълници, което позволява определянето на големината на ъглите.
-
Как се решава задачата за намиране на дължината на диагонала в трапец?
За да намерите дължината на диагонала в трапец, можете да използвате теоремата на Питагор. Първо, трябва да измерите дължините на основите и височината. След това приложете теоремата, за да изчислите дължината на диагонала. Ако е необходимо, можете също да използвате тригонометрични функции за намиране на ъглите в трапеца.
-
Как се решават задачите за намиране на ъгли и дължини в правилна четириъгълна пирамида?
-
Какви са основните принципи при решаването на задачи със симетрия и триъгълници?