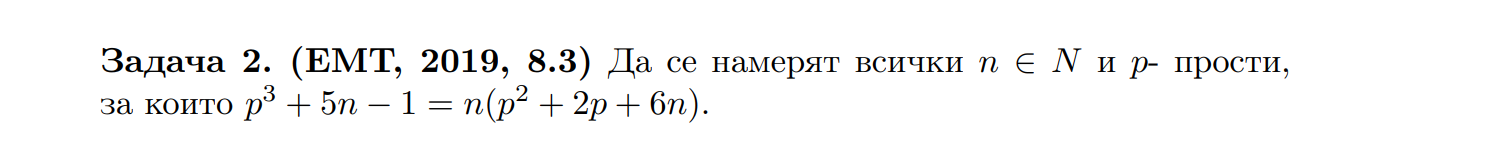Q&A
Обобщени въпроси и отговори от темата *
Какво трябва да се направи? Започнаха ли квадратните уравнения? Или да се разложи на множители?
Как да получите уравненията на другите две страни на успорeнника в задача 1 за 11 клас?
Как да намерите ъгъла между единичните вектори a и b в задача 15 от 11 клас?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Какво трябва да се направи? Започнаха ли квадратните уравнения? Или да се разложи на множители?
-
Как да получите уравненията на другите две страни на успорeнника в задача 1 за 11 клас?
За да намерите уравненията на другите две страни на успорeнника, можете да използвате координатите на точка F(-2,6), която е пресечната точка на диагоналите. След като намерите координатите на върховете на успорeнника, можете да използвате формулата за уравнение на права, която е y = kx + n, където k е наклонът на правата и n е свободният член.
-
Как да намерите ъгъла между единичните вектори a и b в задача 15 от 11 клас?
За да намерите ъгъла между единичните вектори a и b, използвайте дефиницията за скаларно произведение на вектори. След това приложете формулата за скаларно произведение на вектори и определението за единичен вектор, за да намерите ъгъла между тях. В този случай резултатът трябва да бъде 60 градуса, както е посочено в отговора.
-
Как да решим задача за косене на ливада с определена норма?
-
Как да реша диофантово уравнение в цели числа?