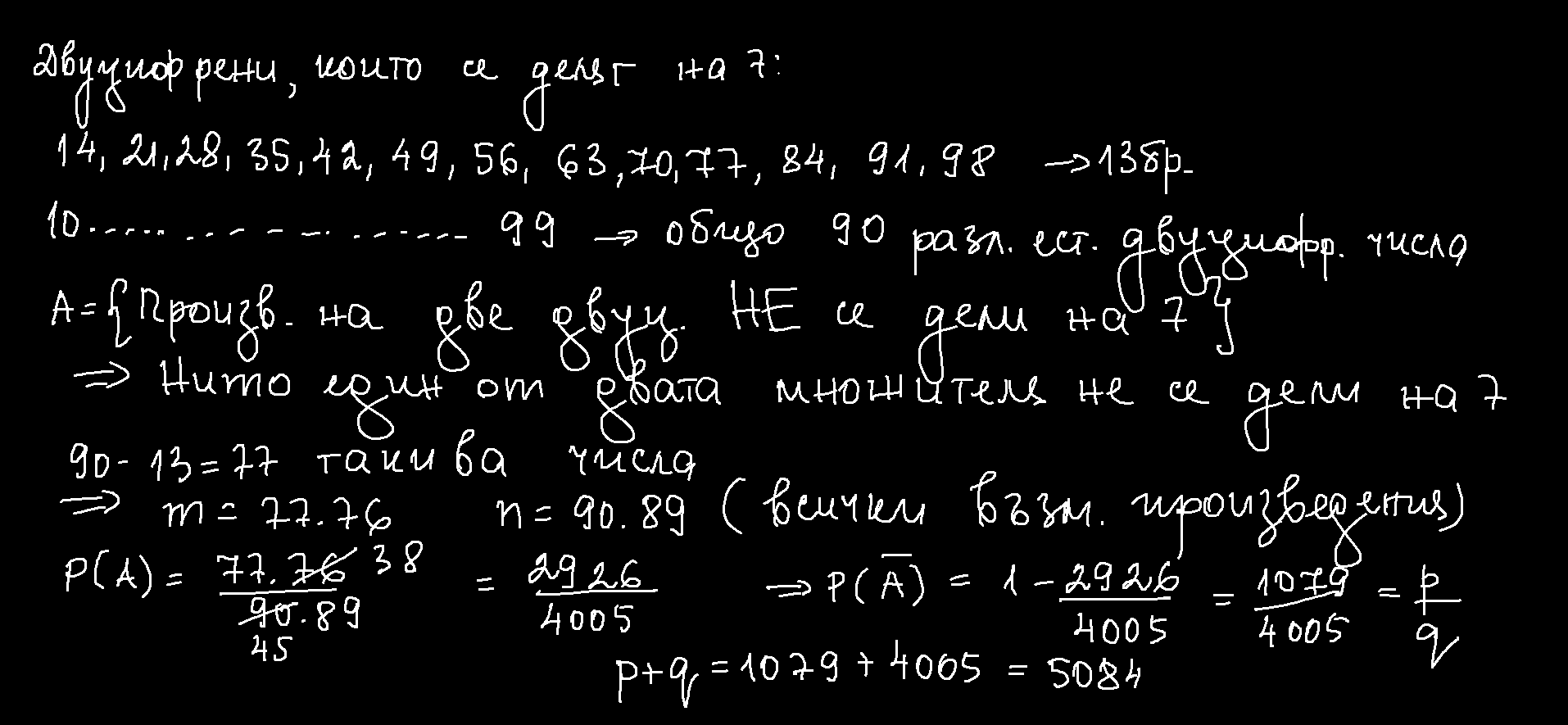Q&A
Обобщени въпроси и отговори от темата *
Как изчисляваме обиколката и ръбовете на правоъгълен паралелепипед?
Как можем да докажем, че лицата на два триъгълника са равни?
Как можем да решим задача с ъглови положения в триъгълник?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Как изчисляваме обиколката и ръбовете на правоъгълен паралелепипед?
Обиколката на основата на правоъгълен паралелепипед е сумата от дължините на неговите страни. Ако знаем, че сборът от всички ръбове е 60 см и имаме обиколката на основата (например 16,8 см), можем да извадим обиколките на двете основи (две по 16,8 см) от общия сбор ръбове. Така изчисляваме измерванията на страничните ръбове и определяме окончателно височината на паралелепипеда.
-
Как можем да докажем, че лицата на два триъгълника са равни?
За да докажем, че лицата на два триъгълника са равни, можем да използваме свойствата на средната отсечка и височините. Ако височините и основите на триъгълниците са равни или свързани, тогава техните лица също ще бъдат равни, тъй като лицето на триъгълник се изчислява по формулата: Лице = (основа × височина) / 2.
-
Как можем да решим задача с ъглови положения в триъгълник?
В задачи с ъглополовящи обикновено е необходимо да се използват свойства на ъглови отношения, за да се намери размерът на определени ъгли. Например, ако знаем, че вътрешните и външните ъглополовящи представят съотношения на равенство, можем да изразим неизвестни ъгли чрез дадените и да намерим търсеното. Важно е да приложите активно разликите и свойствата на подобни триъгълници при решаването.
-
Как се определя обиколката, когато имаме успорeчник?
-
Какви са основните концепции за интеграли, които трябва да знам в 5-6 клас?