Q&A
Обобщени въпроси и отговори от темата *
Какви са необходимите условия за доказване на равенството на триъгълници с помощта на две страни и ъгъл?
Как можем да докажем, че равнобедрен триъгълник с ъглополовяща, равна на медианата, е равнобедрен?
Какви са основните свойства на равнобедрения триъгълник по отношение на медианите, височините и ъглополовящите?
* Предложените въпроси и отговори се генерират машинно от автоматизиран езиков модел на база потребителските мнения в темата. Генерираното съдържание може да е непълно, неактуално, подвеждащо или неподходящо. Вашите оценки спомагат за подобряване на модела и неговото усъвършенстване.
-
Какви са необходимите условия за доказване на равенството на триъгълници с помощта на две страни и ъгъл?
За да се докаже равенството между два триъгълника с помощта на признак за равенство, трябва да се установят две страни и ъгъл между тях от един триъгълник, които са равни съответно на две страни и ъгъл между тях от друг триъгълник. Важно е да се гарантира, че условията са точно зададени, за да се избегнат всякакви нежелани допълнителни построения.
-
Как можем да докажем, че равнобедрен триъгълник с ъглополовяща, равна на медианата, е равнобедрен?
Когато имаме равнобедрен триъгълник, ъглополовящата от ъгъл между равни страни е равна на медианата, която е построена към основата. Тъй като и двете страни на триъгълника са равни, следва, че медианата и ъглополовящата са равни. Когато доказваме тази равенство, можем да използваме свойства на триъгълниците, като например че медианите са равни, което ще доведе до заключение, че триъгълникът е равнобедрен, т.е. всички страни и ъгли са равни.
-
Какви са основните свойства на равнобедрения триъгълник по отношение на медианите, височините и ъглополовящите?
В равнобедрен триъгълник медианите, височините и ъглополовящите през всеки връх са еднакви и се пресичат в една и съща точка. Това свойство е от съществено значение при доказването на равенства между триъгълници, тъй като позволява лесно установяване, че при съвпадащи условия триъгълникът е равнобедрен, а след това и равнинните му елементи.
-
Какви грешки могат да възникнат при доказване на равенства между триъгълници, когато не се използват правилните условия?
-
Как да намерите ъглите на остроъгълен триъгълник, ако някои ъгли са дадени?
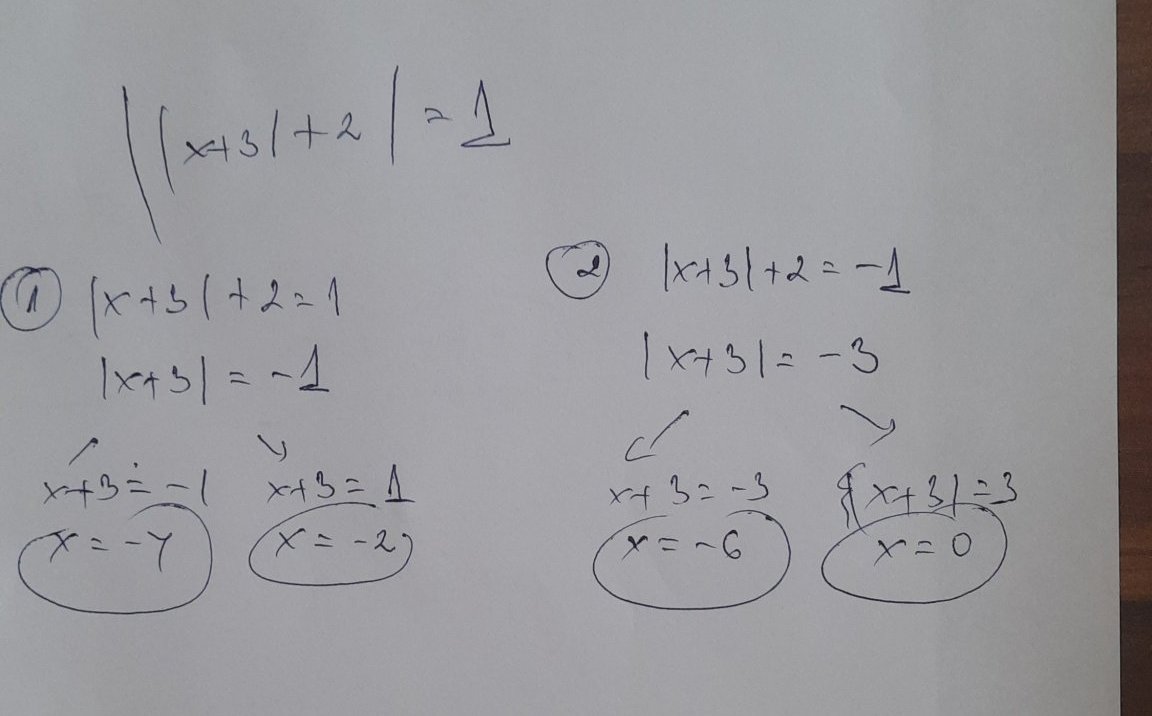



 и окъснях за раЛта....
и окъснях за раЛта....

